Întegral

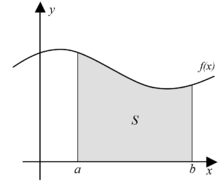
Qada ku di bin munhaniya fonksiyonekê de dimîne, jê re întegral tê gotin. Bi gotineke din jî kirariya dîtinê fonksiyonekê ye, ku darişteya wê tê zanîn lê belê bi xwe nayê zanîn.

Qada ku di bin munhaniya fonksiyonê de û di navbera xalên b û a de dimîne.

Întegral ji aliyê Gottfried Leibniz ve ji bo hesibandina qadên parçeyên biçûk yên bêdawî hatiyê dîtin. Dawêra întegralê  $\int$  e.

Întegral di nav xwe de dibe du beş. Întegrala diyar û întegrala nediyar. Întegrala fonksiyonekê bi alîkariya hin rêzikên sereke ve tê dîtin.

Întegrala hin Fonksiyonan:

$\int {\frac {du}{u}}=\ln \left\vert u\right\vert +C$

$\int u^{n}du={\frac {u^{n+1}}{n+1}}+C,n\neq -1$

$\int udv=uv-\int vdu$

$\int e^{u}du=e^{u}+C$

$\int a^{u}du={\frac {a^{u}}{\ln a}}+C$

Fonksiyonên Trîgonometrîk

$\int \sin udu=-\cos u+C$

$\int \cos udu=\sin u+C$

$\int \sec ^{2}udu=\tan u+C$

$\int \csc ^{2}udu=-\cot u+C$

$\int \sec u\tan udu=\sec u+C$

$\int \csc u\cot udu=-\csc u+C$

$\int \tan udu=\ln \left\vert \sec u\right\vert +C$

$\int \cot udu=\ln \left\vert \sin u\right\vert +C$

$\int \sec udu=\ln \left\vert \sec u+\tan u\right\vert +C$

$\int \csc udu=\ln \left\vert \csc u-\cot u\right\vert +C$

$\int {\frac {du}{\sqrt {a^{2}-u^{2}}}}=\sin ^{-1}{\frac {u}{a}}+C$

$\int {\frac {du}{a^{2}+u^{2}}}={\frac {1}{a}}tan^{-1}{\frac {u}{a}}+C$

$\int {\frac {du}{u{\sqrt {u^{2}-a^{2}}}}}={\frac {1}{a}}sec^{-1}{\frac {u}{a}}+C$

Girêdanên derve

• Malperekê ji bo hesibandina întegralekê

Nimûneyeke hêsan:

Em întegrala $\int (3x^{2}+8x+7)dx$ ê derbixînî.

*hela vê pirsyarê bi formûla duyemîn ya ku li diyar hatiye dayîn tê çareserkirin.

$\int (3x^{2}+8x+7)dx$ = $3{\frac {x^{3}}{3}}+8{\frac {x^{2}}{2}}+7x+C$

=$x^{3}+4x^{2}+7x+C$